Deux livrets d'épargne

Point culture 

Un livret d'épargne fonctionne ainsi : on y dépose une somme d’argent et, chaque année, à la même date, la banque y ajoute des intérêts dont le taux est fixé par le contrat souscrit.
Par exemple, si l'on dépose \(1~000\) € sur un livret avec un taux d’intérêt de \(2{,}4~\%\), le solde après un an sera de \(1~024\) €. L’année suivante, le taux de \(2{,}4~\%\) sera appliqué sur \(1~024\) €, et non sur les \(1~000\) € initiaux, ce qui illustre la notion d’intérêts composés.

Énoncé

Deux amis, Ozan et Julien, se croisent un matin au lycée au retour des vacances de fin d'année. Ils ont, tous les deux, ouvert un livret au taux d'intérêt de \(2{,}4~\%\).

Ozan : Je pense que j'ai fait le bon choix en plaçant tous mes \(10~000\) € économisés dans ce nouveau livret.

Julien : Je viens d'en ouvrir un aussi, mais je ne procède pas de la même manière. Je place \(1~001\) € par an à partir du 1^er janvier 2025. D'après mes calculs, je devrais avoir plus d'argent que toi dessus au bout de 10 ans car \(1~001\times10=10~010\) qui est supérieur à \(10~000\) et, avec les intérêts, j'aurai encore plus !

Ozan : Je ne suis pas sûr que tu aies bien compris le principe des intérêts car ils dépendent de la somme d'argent que tu as ; or, plus la somme est élevée, plus les intérêts le sont également, donc j'aurai plus d'argent. On va détailler les calculs sur les 10 ans à venir.

L'objectif de l'activité est de déterminer qui a raison, autrement dit qui, d'Ozan ou de Julien, aura le plus d'argent sur son livret au bout de 10 ans d'épargne.

Pour simplifier, on supposera que les intérêts s'appliquent directement le 1^er janvier de chaque année et que le taux de \(2{,}4~\%\) reste constant pendant \(10\) ans.

Partie A : modélisation de la stratégie d'Ozan

\(n\) étant un nombre naturel, on pose \((u_n)\) la suite de terme général \(u_n\) représentant l'argent présent sur le livret d'Ozan l'année \((2025+n)\).

1. Donner le premier terme de la suite \((u_n)\).
2. Calculer la somme totale d'argent présente dans le livret d'Ozan en \(2026\).

Coup de pouce : augmenter une quantité d'un certain pourcentage \(t~\%\) revient à multiplier cette quantité par le coefficient multiplicateur \(\left(1+\dfrac{t}{100}\right)\).

3. Calculer \(u_2, u_3\) et \(u_4\). Expliquer pourquoi \((u_n)\) est une suite géométrique et préciser sa raison.
4. Calculer \(u_5\) de deux manières différentes.
5. Combien d'argent Ozan aura-t-il sur son livret en \(2035\) ?

Partie B : modélisation de la stratégie de Julien par un tableur

On va maintenant s'intéresser à la somme d'argent présente sur le livret de Julien au fil des années jusqu'en 2035. Pour rappel, en 2025, Julien verse \(1~001\) €, donc l'argent présent sur le livret est de \(1~001\) €. Puis, chaque année, il verse à nouveau \(1~001\) € tandis que les intérêts de \(2{,}4~\%\) sont calculés et ajoutés à la somme présente l'année précédente.

1. Expliquer pourquoi en 2026 le montant présent, en euros, sur le livret est donné par \(1~001 + 1~001 \times 1{,}024\).
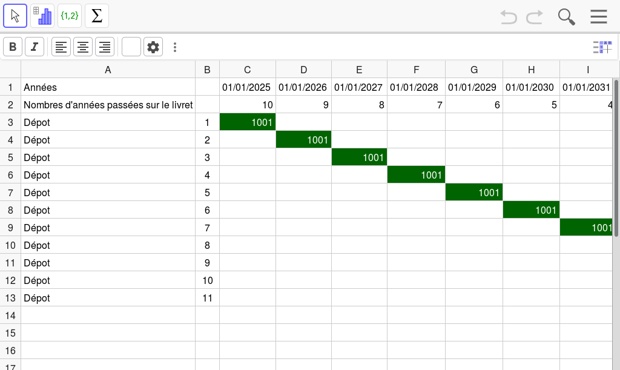
2. Calculer le montant présent sur le livret de Julien en 2027 et en 2028. Le tableur suivant résume la stratégie de Julien.

• La ligne « Nombre d'années passées sur le livret » indique le temps qu'aura passé chacun des versements de Julien sur le livret, et donc combien de fois les intérêts s'appliqueront.
  
• En vert sont indiqués tous les dépôts de \(1~001\) € réalisés depuis l'ouverture du livret.
  
• La case \(\text{D3}\) contient la somme d'argent obtenue en appliquant le taux d'intérêt de \(2{,}4~\%\) aux \(1~001\) € déposés par Julien en ouverture de livret, puisque la ligne \(3\) donne les \(1~001\) € initiaux auxquels s'ajoutent les intérêts au fur et à mesure que les années passent. Par ailleurs, cette ligne ne s'intéresse pas aux versements futurs qui sont donnés par les lignes suivantes.
  
• La colonne \(\text{M}\) contient la somme générée par chaque dépôt annuel de Julien : chaque cellule de la colonne \(\text{M}\) contient les \(1~001\) € ajoutés par Julien chaque année auxquels se sont rajoutés les intérêts. On voit donc que chaque versement aura des intérêts différents puisque ces derniers n'ont pas passé le même temps sur le livret, ce qui rend le calcul de la somme totale plus complexe que pour Ozan.
  

3. Entrer en \(\text{M3}\) la formule \(\text{=C3*1,024^10}\). Que calcule cette formule ?
On dit alors que cette valeur est la valeur acquise par le versement de \(1~001\) € placés en `2025` jusqu'à \(2035\). Compléter le reste de la ligne \(3\) en s'appuyant sur un raisonnement similaire à la cellule \(\text{M}3\).
4. On veut maintenant compléter la ligne \(4\) qui correspond aux \(1~001\) € rajoutés par Julien en 2026. Quelle formule doit-on rentrer en \(\text{E}4\) afin d'obtenir la somme d'argent correspondant ? Compléter la ligne \(4\) en poursuivant le raisonnement.
5. Compléter toute la feuille de calcul de la même manière.
6. À travers ces calculs, on vient de détailler la somme d'argent présente sur le livret. Le but est maintenant de calculer la somme totale. Quelle formule faut-il rentrer dans la case \(\text{M14}\) pour calculer la somme présente sur le livret de Julien en \(2035\) ?
7. Qui aura l'épargne la plus élevée en \(2035\) ?

Partie C : calcul de l'épargne de Julien

Dans le tableur qui modélise la stratégie de Julien, on remarque que tous les termes de la colonne \(\text{M}\) sont des termes d'une suite géométrique de premier terme \(v_0=1~001\) et de raison \(q=1{,}024\). On pose alors \((v_n)\) la suite de terme général \(v_n\) qui donne la valeur acquise de chaque versement de \(1~001\) € au bout de \(n\) années.
Ainsi, par exemple, \(v_5\) représente la valeur acquise par le versement de \(1~001\) € au bout de \(5\) années.
Or la somme totale \(S\) sur le livret en 2035 est la somme de ces valeurs acquises (la valeur acquise par le versement de 2035, puis celle de 2034, … , jusqu'à celle de 2025 qui représente le plus d'argent car elle aura passée 10 ans sur le compte). 
\(S=1~001+1~001\times 1{},024+1~001\times 1{,}024^2+...+1~001\times 1{,}024^{10}\\ S=1~001(1+ 1{,}024+1{,}024^2+...+1{,}024^{10})\\\).
1. Expliquer pourquoi \(1{,}024\times S=1~001(1{,}024+1{,}024^2+1{,}024^3+...+1{,}024^{11})\).
2. Démontrer que \(S-1{,}024\times S=1~001(1-1{,}024^{11})\).
3. Déterminer la valeur de \(S\).
4. De façon générale, soit \(q\) un nombre positif, avec \(q\ne 1\), et \(n\) un entier naturel.
Démontrer que \(q^0+q^1+q^2+...+q^n=\dfrac{1-q^{n+1}}{1-q}\).